Transpose

转置

假设我们有一个矩阵

A = (\begin{matrix} 5 & 6 \\ 9 & 4 \end{matrix})

它表示了从 $2$ 维到 $2$ 维空间的变换，对应任意的 $m \cdot n$ 矩阵，都表示一个从 n 维空间到 m 维空间的变换，例如我们有一个 $1 \cdot 2$ 矩阵 $(\begin{matrix} 1 & - 2 \end{matrix})$ ，它表示了一个从2维空间到1维空间的变换，如图中我们可以看到 $(1, - 2)$ 变换到了 $- 1$

可以想象成一部机器，喂入两个数，得到一个数，具体的操作过程与投影projection有关,就像一个小人在数轴上，先移动了

1

步，然后又移动了

- 2

步，那么最终看来，这个小人只移动了

- 1

步,即后退了一步

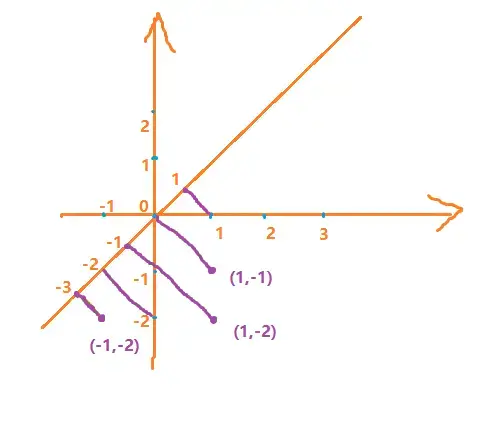
而转置呢，操作上来说就是行变为列，列变成行，转了一下，例如

(\begin{matrix} 1 & - 2 \end{matrix})

转过来就是

(\begin{matrix} 1 \\ - 2 \end{matrix})

(即我们应当结合维度变换的角度去理解转置)

将这些操作转换成代数上就是

(\begin{matrix} 1 & - 2 \end{matrix}) \cdot (\begin{matrix} 1 \\ 1 \end{matrix}) = 1 \cdot 1 + (- 2 \cdot 1) = - 1

我们使用 $\cdot$ 这个小点来表示这种"走了1步，又走了-2步"这种计算，而这种计算呢，又恰巧就是我们待会要讲到的点乘dot_product

补充：关于更加详细的坐标变换，线性代数的本质【搬运】【线性代数】线性代数的本质_哔哩哔哩_bilibili