Perspective transformation

透视变换Perspective Transformation

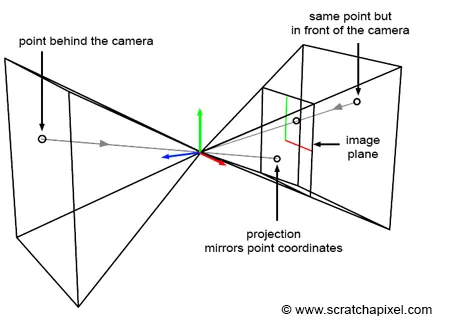
什么是透视变换？图片透视变换是一个投影过程，其中透视变换就像将人的眼睛当做一个中心点，外部世界是一个大平面，在眼睛与这个平面之间形成一个椎体，然后将这个平面上的内容投射到眼睛内。

为什么变换之后的空间被称为裁切空间？裁切就是把不需要的部分去除掉，就是这幅图片中一样，投影平面在左侧

而在投影中心另一侧的右侧的点我们是不需要的，假设这个点的坐标为

(2, 5, 10)

应用计算之后是

x^{'} = \frac{2}{- 10} = - 0.2

y^{'} = \frac{5}{- 10} = - 0.5

z^{'} = \frac{10}{- 10} = - 1

那么这个计算过程是如何进行的呢？根据相似三角形

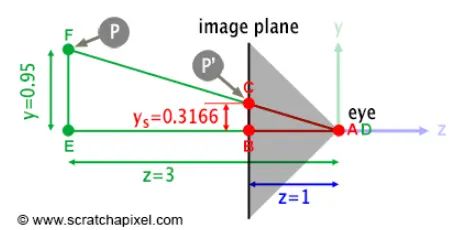
Figure 1 (从P投射到P')

我们有

\frac{B A = z_{b l u e} = 1}{E A = z_{g r e e n} = 3} = \frac{B C = y^{'}}{E F = y}

y^{'} = \frac{y * z_{b l u e}}{z_{g r e e n}}

其中，由于我们的摄像机是看向 $- z$ 方向的，所以 $z_{g r e e n}$ 在计算的时候前面要加 $-$ 号，这就是式子 $y^{'} = \frac{5}{- 10} = - 0.5$ 中 $z$ 的值为 $10$ ，计算是为 $- 10$

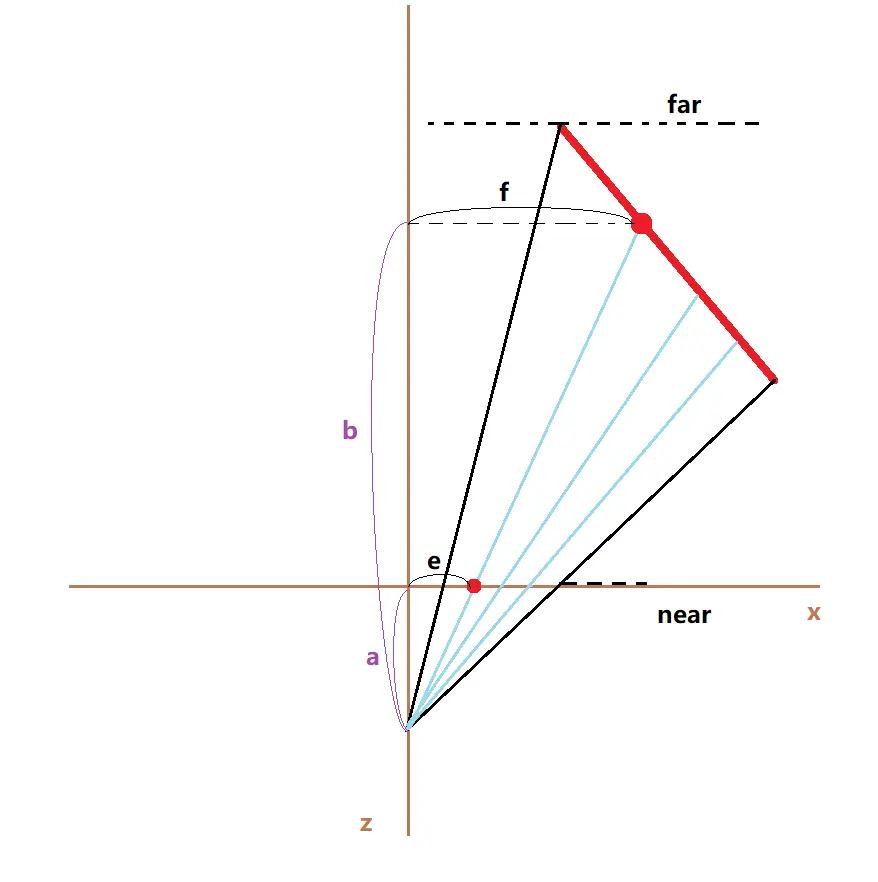
Look at the projection from another aspect

步骤

假设我们有一个矩阵

\begin{array}{r} [\begin{array}{c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}] \end{array}

我们先让 $z$ 坐标分量等于 $- 1$ ,这样计算后的 $z^{'}$ 就等于 $1$ ,就可以满足如Figure 1中的

z^{'} = z = 1

接下来，再调整 $w$ 分量从

[0, 0, 0, 1] \to [0, 0, - 1, 0]

这样一来,当除以 $w$ 分量从齐次转三维中的点时，除以 $w$ 分量相当于除以了 $- z$ 分量，经过这样调整后我们有

\begin{array}{r} [\begin{array}{c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & - 1 & - 1 \\ 0 & 0 & 0 & 0 \end{array}] \end{array}

其计算过程正好是我们想要的

\begin{array}{r} (\begin{array}{c} x^{'} & = x \cdot 1 + y \cdot 0 + z \cdot 0 + 1 \cdot 0 = x \\ y^{'} & = x \cdot 0 + y \cdot 1 + z \cdot 0 + 1 \cdot 0 = y \\ z^{'} & = x \cdot 0 + y \cdot 0 + z \cdot (- 1) + 1 \cdot 0 = - z \\ w^{'} & = x \cdot 0 + y \cdot 0 + z \cdot (- 1) + 1 \cdot 0 = - z \end{array} \end{array}

\begin{array}{ll} x^{'} = \frac{x^{'} = x}{w^{'} = - z}, \\ y^{'} = \frac{y^{'} = y}{w^{'} = - z}, \\ z^{'} = \frac{z^{'} = - z}{w^{'} = - z} = 1. \end{array}

其中 $z^{'} = \frac{z}{w} = \frac{- z}{- z} = 1$ ,　　 $x^{'} = \frac{x}{w} = \frac{x}{- z}$ ,　　 $y^{'} = \frac{y}{w} = \frac{y}{- z}$ 接下来我们就需要详细计算每个部分了

[\begin{array}{cccc} \frac{2 n}{r - l} & 0 & . . . & 0 \\ 0 & \frac{2 n}{t - b} & . . . & 0 \\ \frac{r + l}{r - l} & \frac{t + b}{t - b} & . . . & - 1 \\ 0 & 0 & . . . & 0 \end{array}]

(我们根据齐次转三维点时, $(x, y, z)$ 这三个分量都要除以 $w$ 分量，我们有

(x^{'}, y^{'}, z^{'}) = (x / w, y / w, z / w)

其中 $x$ 和 $y$ 对 $z$ 无影响)，则上一步骤中的矩阵可以设为

[\begin{array}{cccc} \frac{2 n}{r - l} & 0 & 0 & 0 \\ 0 & \frac{2 n}{t - b} & 0 & 0 \\ \frac{r + l}{r - l} & \frac{t + b}{t - b} & A & - 1 \\ 0 & 0 & B & 0 \end{array}]

其中A和B是我们要求的,则可以列出等式

z^{'} = \frac{0 * x + 0 * y + A * z + B * w}{w = - z} \to \frac{A z + B}{w = - z} .

注意这里的 $w = 1$ 是 $(x, y, z, w = 1)$ 中的 $w$ ，而不是这个矩阵中的 $w$ 分量
再根据我们已知 $z$ 正好落在 $n e a r$ 近平面时应当等于 $- 1$ ，正好落在 $f a r$ 远平面时应当等于 $1$ , 我们可以列出式子

(\begin{array}{ll} \frac{(z = - n) A + B}{(- z = - (- n) = n)} = - 1 & when z = n \\ \frac{(z = - f) A + B}{(- z = - (- f) = f)} = 1 & when z = f \end{array}

\to (\begin{array}{ll} - n A + B = - n & (1) \\ - f A + B = f & (2) \end{array}

A = - \frac{f + n}{f - n}

B = - \frac{2 f n}{f - n}

(也可以映射到[0,1]范围内)

补充资料

将原来透视矩阵中的 $(0, 0, 0, 1)$ 变为 $(0, 0, - 1, 0)$ 之后, 就说当我们用这个透视矩阵的 $w$ 分量乘以一个齐次点

(x, y, z, 1)

时，我们有

x \cdot 0 + y \cdot 0 + z \cdot - 1 + 1 \cdot 0 = - z

也就是说，这个齐次点 $w$ 的值经过矩阵计算之后从之前的 $1$ 变为了 $- z$ ,同时，齐次点 $(x, y, z)$ 变为三维点时需要经过 $(x / w, y / w, z / w)$ ，此时这样就有

(x / w, y / w, z / w) \Rightarrow (x / - z, y / - z, z / - z)

因为摄像机是朝向 $- z$ 方向的，所以摄像机前所有的点的 $z$ 坐标都是负的，这就是为什么【资料1】中

x^{'} = \frac{x}{- z}

中的 $z$ 前方带有负号

透视变换矩阵

\begin{array}{r} M_{p e r s p} = [\begin{array}{c} \frac{2 n}{r - l} & 0 & \frac{l + r}{l - r} & 0 \\ 0 & \frac{2 n}{t - b} & \frac{b + t}{b - t} & 0 \\ 0 & 0 & \frac{f + n}{f - n} & \frac{2 n f}{n - f} \\ 0 & 0 & 1 & 0 \end{array}] \end{array}

或

\begin{array}{r} M_{p e r s p} = [\begin{array}{c} \frac{2 n}{r - l} & 0 & 0 & 0 \\ 0 & \frac{2 n}{t - b} & 0 & 0 \\ \frac{r + l}{r - l} & \frac{t + b}{t - b} & - \frac{f + n}{f - n} & - 1 \\ 0 & 0 & - \frac{2 n f}{n - f} & 0 \end{array}] \end{array}

(注意其中两者之间的负号)

则我们有

[x^{'}, y^{'}, z^{'}, w^{'}] = [\begin{matrix} x \\ y \\ z \\ w = 1 \end{matrix}] * M_{p e r s p}

其中

w^{'} = 0 \cdot x + 0 \cdot y - 1 \cdot z + 0 \cdot 1 = - z

计算并验证一下，假设 $n = 1 ， f = 20$ 公式

\frac{- \frac{f + n}{f - n} * z - \frac{2 f n}{f - n}}{- z}

代入 $n$ 和 $f$ 并计算得

\frac{- \frac{21}{19} * z - \frac{40}{19}}{- z}

其中 $\frac{- 21}{19} = - 1.1$ 和 $\frac{- 40}{19} = - 2.1$ 则得到结果

z = 1 \to \frac{- 1.1 * 1 - 2.1}{- 1} = 3.2

z = - 1 \to \frac{- 1.1 * - 1 - 2.1}{1} = - 1

z = - 20 \to \frac{- 1.1 * - 20 - 2.1}{20} = 0.995

z = - 21 \to \frac{- 1.1 * - 21 - 2.1}{21} = 1.1