Linear transforms and translation
线性变换Linear Transforms
缩放Scale
非均匀缩放 Scale (Non-Uniform)
反射Reflection
错切Shear
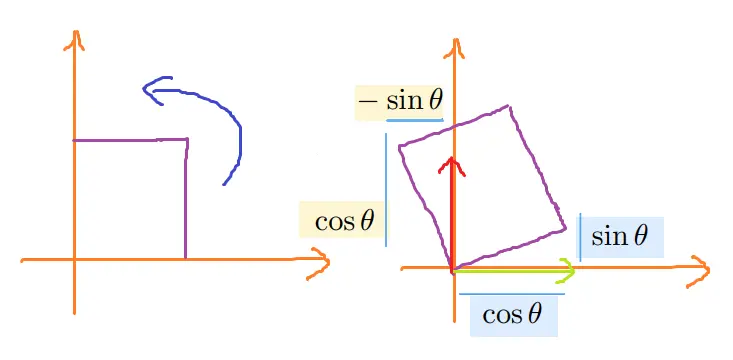
旋转Rotate
**平移Translation
平移
平移不是一个线性变换,它是一个仿射变换,因为线性变换其中的一个特性就是变换前后坐标系的原点保持不变,显然平移不满足这个特性;或者还可以说我们无法用一个矩阵去描述这个变换,不像之前的旋转缩放等变换我们都可以用一个矩阵就可以描述。再从另外一个角度来描述就是我们"无法通过只使用乘法来描述这个变换"
我们假设一个场景,在一维情景下,我们有一个数轴,还有三个点在
处,我们想要将这三个点往右移动一个单位,也就是
这是对这三个点都使用"+1"这个一个同样的操作我们做到了,那么我们可不可以使用乘法呢?我们观察到,
所以,Translation我们需要使用这种方式来表示
可这样表示后面会多出
使得偏偏平移变换与其它的变换不同,那有没有其它的方法呢?答案是: homogenous_coordinates 齐次坐标
变换复合
complex_transformation变换复合,很容易就理解
Here[1]
3维下
For math render, we use
\mathbf{T}\_{x}instead of\mathbf{T}_{x}, But some doesn't support. ↩︎