Equation and determinant
方程与行列式
有一个方程,我们试着解一下
我们用消去法
最终可以得到
大家有没有注意到
他们是一样的,所以为了简化计算,我们将这个
这样一组数,再定义
叫做行列式, 而
也是方程中的系数(称作系数矩阵),通用格式就是
再看另外一个方程
列出系数矩阵形式
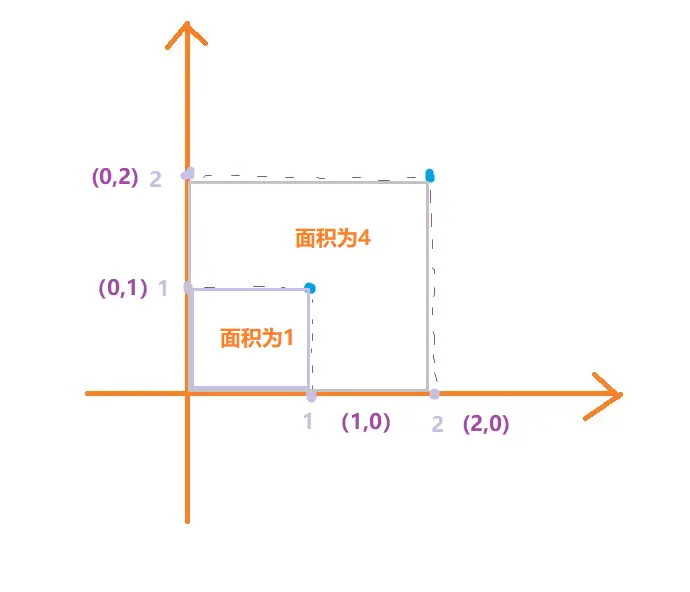
观察图中我们看到如果我们把
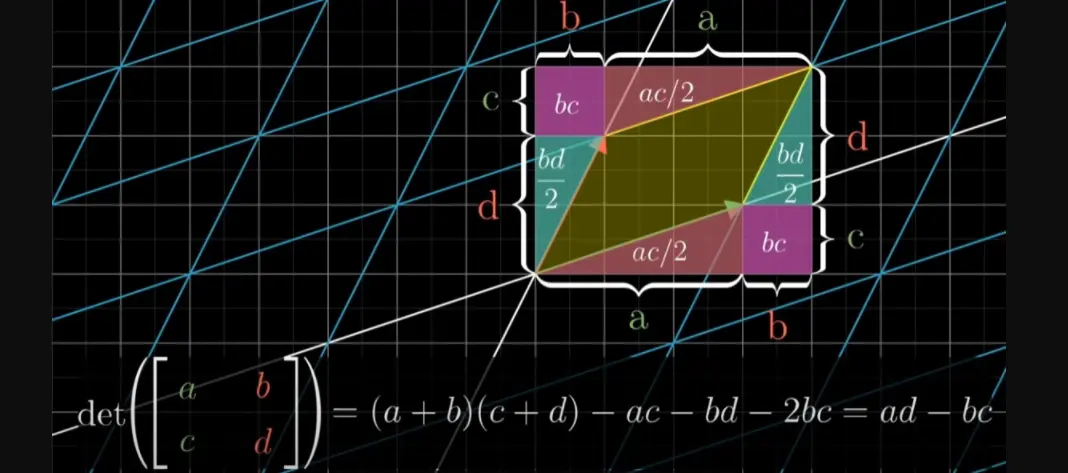
我们两个坐标
现在形成的面积是一个平行四边形,经过计算后我们发现也满足。
方程与行列式
有一个方程,我们试着解一下
我们用消去法
最终可以得到
大家有没有注意到
他们是一样的,所以为了简化计算,我们将这个
这样一组数,再定义
叫做行列式, 而
也是方程中的系数(称作系数矩阵),通用格式就是
再看另外一个方程
列出系数矩阵形式

观察图中我们看到如果我们把

我们两个坐标
现在形成的面积是一个平行四边形,经过计算后我们发现也满足。