Equation and coordinate axis

方程中的等号是问题的核心，方程（英文：equation）是表示两个数学式（如两个数、函数、量、运算）之间相等关系的一种等式，而函数的定义是在非空数集之间的映射称为函数，要注意区分

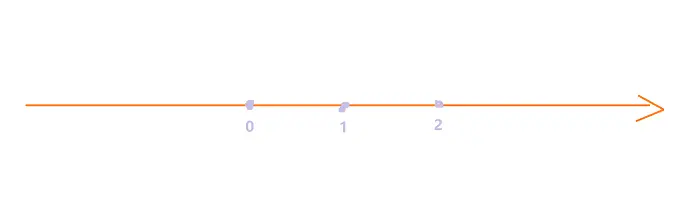
我们先定义坐标轴这个家伙，首先定义一条直直的线，然后我们再在这条线上定义一些单位，也就是刻度(1,2,3...)等，这些都是我们定义的，刻度 $1$ 可以代表任何事物，例如一个苹果，移动了一米等等都可以，而这条直线呢，也是我们定义的，就像我们走路都是直直的前往某个地方，所以为了刻画这种东西，所以我们定义坐标轴也为直的，如果我们每个人都走路是沿曲折的曲线前进，那么我们的坐标轴估计也就是弯弯曲曲的了 (只是猜测)，好了，我们定义完了"坐标轴"，来看一个例子

首先让我们来思考个问题，先假设 $(0,)$ 到 $(1,)$ 之间表示 $1$ 米，假设小红站在 $(0,)$ 点不动，小明从 $(0,)$ 出发走到了 $(2,)$ 这个位置，走了 $2$ 米，请问，小红需要走多少个 $1$ 米就可以达到小明现在的位置，我们假设需要走 $x$ 个 $1$ 米就可以达到小明的位置，表现为方程就是 $1 x = 2, x = 2$ ,小红需要走 $2$ 个 $1$ 米这么长的距离才可以达到小明的位置，这就是方程，描述两个事物之间的相等关系，其中等号是核心，只不过在一维情况下，比较简单，到了二维时，就要稍微复杂那么一丢丢了

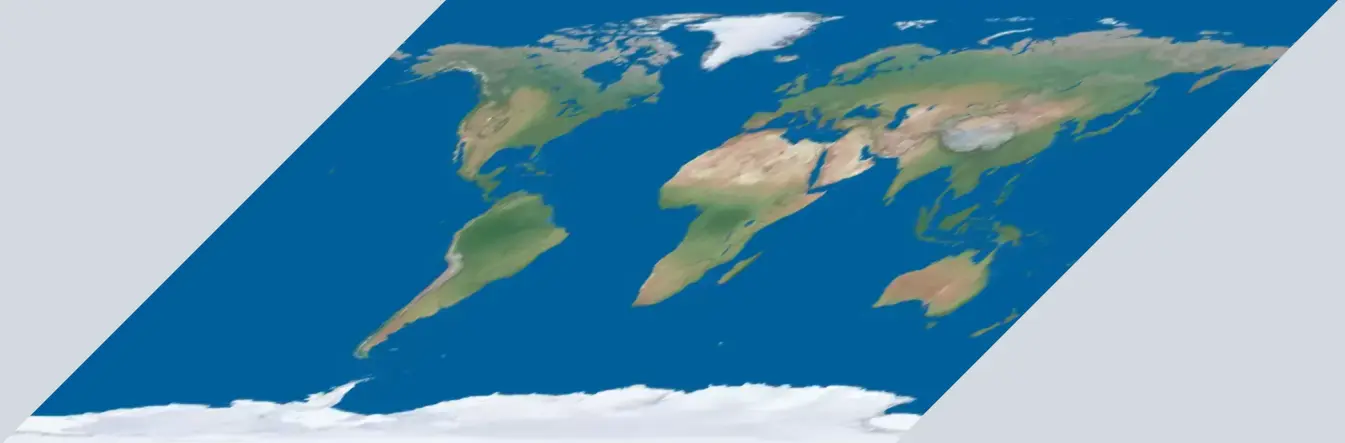
这里举一个简单的二维情况下，我们还是以小明和小红走路这个例子为例，前面是在数轴上，他们可以活动的范围太小了，只在一条线上，我们现在把它扩大到一个平面上，现在取两条数轴，还有刻度，然后再让这两条数轴垂直，像 $(x, y)$ 那样，那么能不能斜着呢？可以，只不过这些都是与我们的生活相贴近的，就像展开的地球，如果我们生活的地方就像第二张被错切之后的那样,其中的任何事物都是错切的形状，那估计我们的坐标系也就是会是那样定义了，就像 $(x^{'}, y^{'})$ 那样 (只是猜测)

(二维坐标系，两条不相互垂直的坐标轴，就像我们所生活的世界，我们在一个巨大的平面上)

现在把这两个数轴放到一个平面中去，那么我们的维度就上升了一个层面，定义完之后，也就是说，我们不仅可以左右移动了，也可以上下移动了

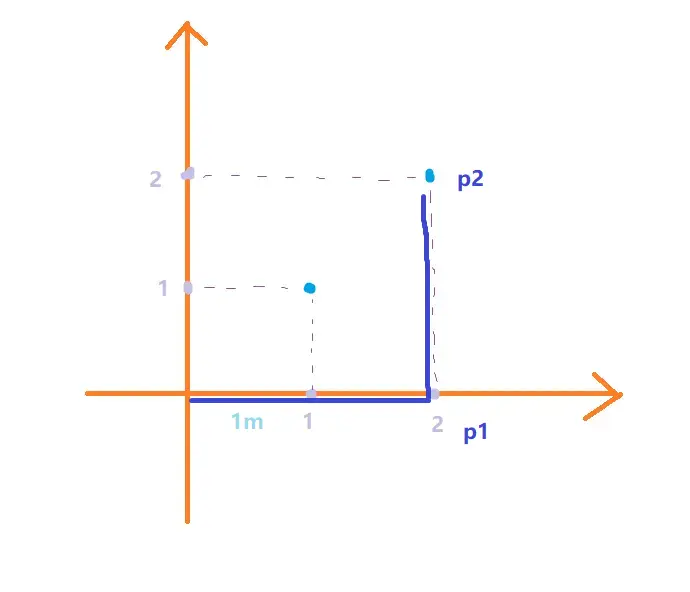
假设我们在 $(0, 0)$ 点，想要前往到 $(2, 2)$ 点，我们能想象得到也比较直观的就是，沿着左右方向中的右那个方向走 $2$ 个单位，然后再沿着上下方向中的上那个方向走 $2$ 个单位，就到了 $(2, 2)$ ，你们可能想，这也太麻烦了，我直接从 $(0, 0)$ 到 $(2, 2)$ 之间连一条线，然后沿着那条线走不就行了嘛，是的，这就是极坐标系的由来，我们看待同一种问题的不同视角，这里我们先讨论直角坐标系

回到问题， $(0, 0) \to (2, 2)$ , 分开来看，就是先往右移动 $2 m$ 到达 $p 1$ ，再往上移动 $2 m$ 到达 $p 2$ ，设往右移动 $x$ 个 $1 m$ 才能到达 $p 1$ 处,然后往上移动 $y$ 个 $1 m$ 才能到达 $p 2$ 处, 则我们有

\begin{array}{l} (\begin{array}{c} 1 x = 2 \\ 1 y = 2 \end{array} \\ (\begin{array}{c} x = 2 \\ y = 2 \end{array} \end{array}

往右移动 $2$ 个 $1 m$ 才能到达 $p 1$ 处，然后往上移动 $2$ 个 $1 m$ 才能到达 $p 2$ 处。