Dot product

点乘我们通常用于衡量两个向量的方向差，或者衡量"做功"的大小，通常我们将它们单位化，然后再计算，这样取值范围就在 $- 1$ 到 $1$ 之间，例如两个向量共向，那么值为 $1$ ，反向则为 $- 1$ ，垂直为 $0$

代数定义

两个向量 $\vec{a} = [a_{1}, a_{2}, \dots, a_{n}]$ 和 $\vec{b} = [b_{1}, b_{2}, \dots, b_{n}]$ 的点积定义为

\begin{array}{r} \vec{a} \cdot \vec{b} = \sum_{i = 1}^{n} a_{i} b_{i} \end{array}

其中 $n$ 是维度，在2维情况下就是 $a_{1} b_{1} + a_{2} b_{2}$ ,例如

(\begin{matrix} 5_{(a_{1})} & 6_{(b_{1})} \\ 9_{(a_{2})} & 4_{(b_{2})} \end{matrix})

就是 $5 \times 6 + 9 \times 4$ （这里需要注意与行列式的计算是不一样的，行列式是 $5 \times 4 - 6 \times 9$ ）这里点乘的计算和我们在转置那里讲到的投影是一回事

几何定义
在欧几里得空间中，点积可以直观地定义为

\vec{a} \cdot \vec{b} = | \vec{a} | | \vec{b} | \cos θ

其中 $θ$ 为两向量之间的夹角

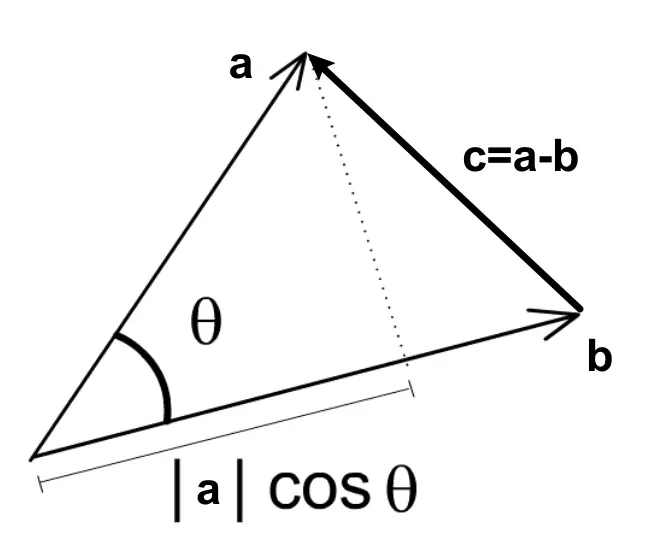
推导

两个定义之间是等价的并可以互相推出
根据cosine_law余弦定理则我们有

| | a - b | |^{2} = | | a | |^{2} + | | b | |^{2} - 2 | | a | | | | b | | c o s α

展开得

\begin{array}{r} \sum_{i = 1}^{n} (a_{i} - b_{i})^{2} = \sum_{n}^{i = 1} a_{i}^{2} + \sum_{n = 1}^{n} b_{i}^{2} - 2 | | a | | | | b | | c o s α \end{array}

Here^[1]

在二维情况下展开有

\begin{array}{r} (a_{1}^{2} + b_{1}^{2} - 2 a_{1} b_{1}) + (a_{2}^{2} + b_{2}^{2} - 2 a_{2} b_{2}) = a_{1}^{2} + a_{2}^{2} + b_{1}^{2} + b_{2}^{2} - 2 | | a | | | | b | | c o s α \end{array}

消去所有的 $a_{1}^{2}, b_{1}^{2}$ 整理后有

- 2 a_{1} b_{1} + (- 2 a_{2} b_{2}) = - 2 | | a | | | | b | | c o s α

两边再同除以 $- 2$ 有

a_{1} b_{1} + (a_{2} b_{2}) = | | a | | | | b | | c o s α = \vec{a} \cdot \vec{b}

同样可以推广到 $n$ 维 □

点乘在投影上的应用

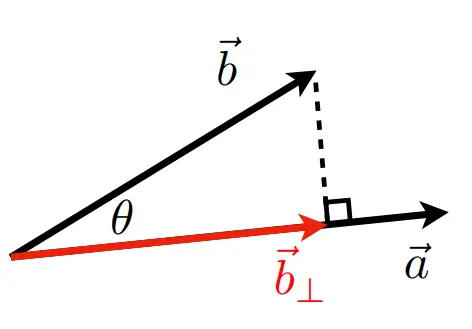
计算出向量 $\vec{b}$ 在 $\vec{a}$ 上的投影值,则有 $| | {\vec{b}}_{⊥} | | = | | \vec{b} | | c o s θ$

when display $$xxx$$ not rendered. cause of have things like \sum^{n}_{i=1}, must replace with \sum^{n}\_{i=1} 2. Or use _ first then use ^ second. e.g. \sum_{i=1}^{n} ↩︎