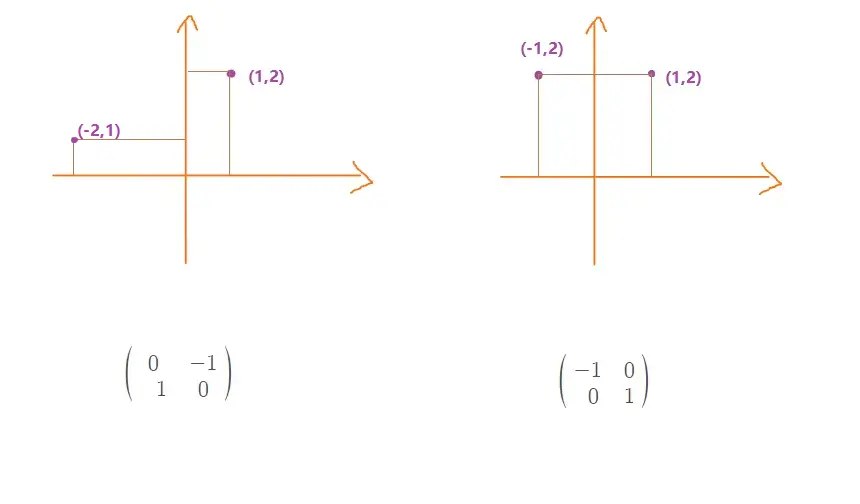Cross product

叉乘只在三维中有定义，两个向量的叉乘可以产生一个与这两个向量都垂直的新向量。例如计算一个物体表面的法向量

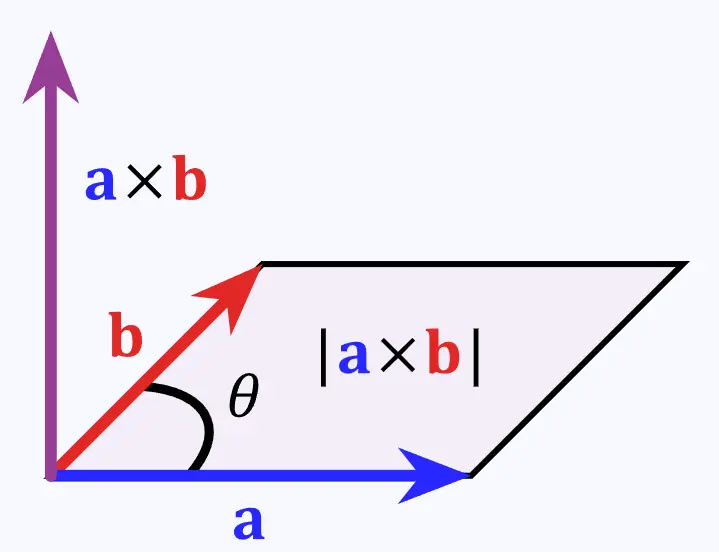
叉乘定义

a \times b = ‖ a ‖ ‖ b ‖ \sin (θ) n

其中 $θ$ 表示 $a$ 向量和 $b$ 向量之间的夹角，而 $n$ 则是一个与 $a$ 、 $b$ 所构成的平面垂直的单位向量，方向由右手定则决定 (https://zh.wikipedia.org/wiki/叉积)

模长计算

‖ a \times b ‖ = ‖ a ‖ ‖ b ‖ \sin (θ)

模长等于以两个向量为边的平行四边形的面积

叉乘计算

Part1
叉乘计算规则：如果两个向量一样，叉乘结果为 $0$
通过引入单位向量，向量就可以转化成代数形式，例如

a = a_{1} i + a_{2} j + a_{3} k, b = b_{1} i + b_{2} j + b_{3} k

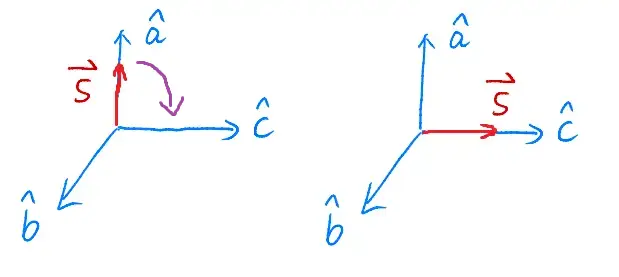
$i ， j ， k$ 是三个相互垂直的向量。它们刚好可以构成一个坐标系。这三个向量就是

i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1)

Part2

a = (a_{1}, a_{2}, a_{3}), b = (b_{1}, b_{2}, b_{3})

分别为两三维向量，叉乘为

a \times b = < a_{2} b_{3} - a_{3} b_{2}, a_{3} b_{1} - a_{1} b_{3}, a_{1} b_{2} - a_{2} b_{1} >

也可以写成伪行列式的形式equation_and_determinant

a \times b = (\begin{matrix} i & j & k \\ a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{matrix}) = i (a_{2} b_{3} - a_{3} b_{2}) + j (a_{3} b_{1} - a_{1} b_{3}) + k (a_{1} b_{2} - a_{2} b_{1})

a \times b = (\begin{matrix} a_{2} b_{3} - a_{3} b_{2} \\ a_{3} b_{1} - a_{1} b_{3} \\ a_{1} b_{2} - a_{2} b_{1} \end{matrix})

Part3
先以二维为例，假设有一个向量 $a = (a_{1}, a_{2})$ 然后我们引入反对称矩阵

H = (\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix})

然后计算

a H a^{T}

得结果为

(\begin{matrix} a_{1} & a_{2} \end{matrix}) (\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix}) (\begin{matrix} a_{1} \\ a_{2} \end{matrix}) = (\begin{matrix} a_{1} & a_{2} \end{matrix}) (\begin{matrix} - a_{2} \\ a_{1} \end{matrix}) = (\begin{matrix} a_{1} (- a_{2}) + a_{2} a_{1} \end{matrix}) = 0

由叉乘的规则我们有

a \times a = [a]_{\times} * a = 0

其中 $[a]_{\times}$ 表示某个叉乘矩阵，然后作用到了 $a$ 得结果为 $0$ ,通过对比，我们可以发现， $a H$ 就是向量a的叉乘矩阵，当 $a$ 为列向量时， $a^{T} H$ 为a向量的叉乘矩阵，如果向量 $a = (a_{1}, a_{2}, a_{3})$ 为三维向量，那么H为

H = (\begin{matrix} H_{1} \\ H_{2} \\ H_{3} \end{matrix}) H_{1} = (\begin{matrix} 0 & 0 & 0 \\ 0 & 0 & - 1 \\ 0 & 1 & 0 \end{matrix}) H_{2} = (\begin{matrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ - 1 & 0 & 0 \end{matrix}) H_{3} = (\begin{matrix} 0 & - 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{matrix})

最后将变换合并起来就是

H = (\begin{matrix} 0 & - 1 & 1 \\ 1 & 0 & - 1 \\ - 1 & 1 & 0 \end{matrix})

则最终有

a H = (\begin{matrix} 0 & - a_{3} & a_{2} \\ a_{3} & 0 & - a_{1} \\ - a_{2} & a_{1} & 0 \end{matrix})

a \times b = A * b = (\begin{matrix} 0 & - a_{3} & a_{2} \\ a_{3} & 0 & - a_{1} \\ - a_{2} & a_{1} & 0 \end{matrix}) (\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix})

Part4
根据内积和外积的定义 dot_product

(a \times b) \cdot a =< a_{2} b_{3} - a_{3} b_{2}, a_{3} b_{1} - a_{1} b_{3}, a_{1} b_{2} - a_{2} b_{1} > \cdot a = a_{1} (a_{2} b_{3} - a_{3} b_{2}) + a_{2} (a_{3} b_{1} - a_{1} b_{3}) + a_{3} (a_{1} b_{2} - a_{2} b_{1})

= a_{1} a_{2} b_{3} - a_{1} a_{3} b_{2} + a_{2} a_{3} b_{1} - a_{2} a_{1} b_{3} + a_{3} a_{1} b_{2} - a_{3} a_{2} b_{1} = 0

假设有两个不共线的向量，分别为 $(a_{1}, a_{2}, a_{3}), (b_{1}, b_{2}, b_{3})$ ,我们设我们要找的垂直于这两个向量的向量为 $(x, y, z)$ ，那么我们则有如下方程

(\begin{matrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{matrix}) (\begin{matrix} x \\ y \\ z \end{matrix}) = (\begin{matrix} 0 \\ 0 \end{matrix}) = 0

\Rightarrow (\begin{matrix} a_{1} x + a_{2} y + a_{3} z = 0 \\ b_{1} x + b_{2} y + b_{3} z = 0 \end{matrix}

There is a footnote here ^[1]

(这里可以看做向量 $(a_{1}, a_{2}, a_{3})$ 和 $(b_{1}, b_{2}, b_{3})$ 分别与要求向量 $(x, y, z)$ 的点乘，如果垂直点乘结果为 $0$ ) 令式子中的 $z = 1$ ,则我们有

(\begin{matrix} a_{1} x + a_{2} y = - a_{3} (1) \\ b_{1} x + b_{2} y = - b_{3} (2) \end{matrix}

因为我们的方程组的秩小于未知数的个数，这里不妨设 $z = 1$ 然后再求解)
然后解二元一次方程，另 $(1) \times \frac{b_{1}}{a_{1}} - (2)$ 得

y = \frac{a_{1} b_{3} - a_{3} b_{1}}{a_{2} b_{1} - a_{1} b_{2}}

与

x = \frac{a_{3} b_{2} - a_{2} b_{3}}{a_{2} b_{1} - a_{1} b_{2}}

因此所求向量为

(\frac{a_{3} b_{2} - a_{2} b_{3}}{a_{2} b_{1} - a_{1} b_{2}}, \frac{a_{1} b_{3} - a_{3} b_{1}}{a_{2} b_{1} - a_{1} b_{2}}, 1)

改变一下形式我们有

(a_{3} b_{2} - a_{2} b_{3}, a_{1} b_{3} - a_{3} b_{1}, a_{2} b_{1} - a_{1} b_{2})

这个形式与之前的形式相差了一个 $-$ 号，还有另外一种解法使用 $(2) \times \frac{a_{1}}{b_{1}} - (1)$ 所得的结果的形式与之前的形式相同

补充(https://github.com/Krasjet/quaternion/blob/master/quaternion.pdf)

叉乘的定义在历史顺序上来说是从Graßmann积中导出

For math render, use \begin{cases} instead of \left { that doesn't supported. Or use \left ( with end of \right. ↩︎