Coordinate basis vector and transformation
坐标基矢
坐标基矢是我们人为定义的事物;一维情形下就是数轴上
二维有两个坐标轴,分别为
叫做
叫做
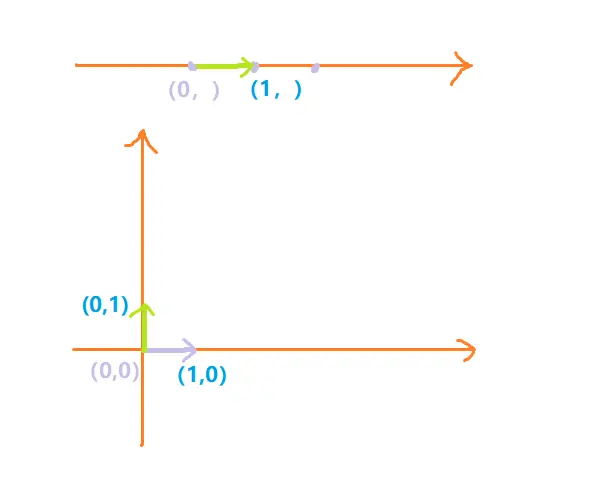
刚才我们未引入坐标基矢,引入坐标基矢后,现在就有了一种统一的形式,上述例子的完整情况为
矩阵形式
其实我们可以看到,我们想要去到的那个点
都应想起是笛卡尔坐标系中的两个坐标基矢的变换, 像
可以看做
只不过这两个坐标基没有产生任何的变化; 再如
可以看做
为了便于描述,我们还通常给我们要去的
坐标基矢
坐标基矢是我们人为定义的事物;一维情形下就是数轴上
二维有两个坐标轴,分别为
叫做
叫做

刚才我们未引入坐标基矢,引入坐标基矢后,现在就有了一种统一的形式,上述例子的完整情况为
矩阵形式
其实我们可以看到,我们想要去到的那个点
都应想起是笛卡尔坐标系中的两个坐标基矢的变换, 像
可以看做
只不过这两个坐标基没有产生任何的变化; 再如
可以看做
为了便于描述,我们还通常给我们要去的