Bezier Curve
Graphics-Bezier Curve
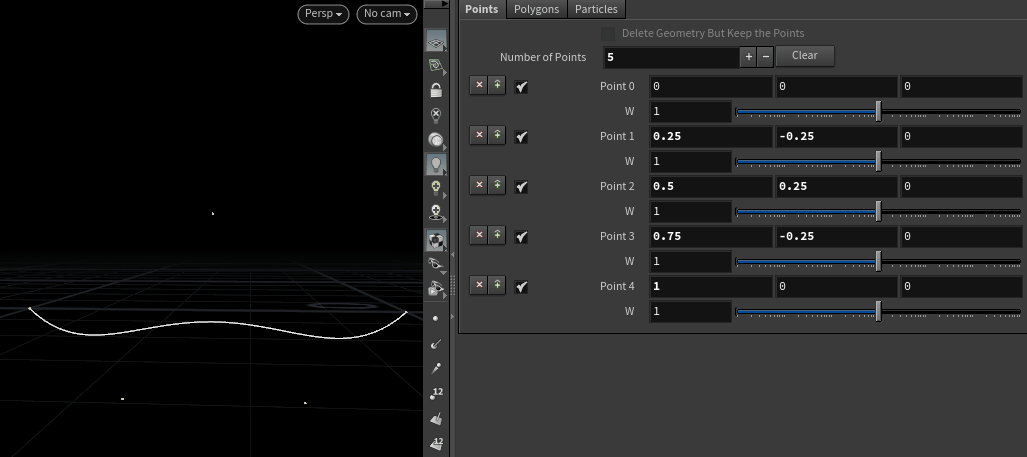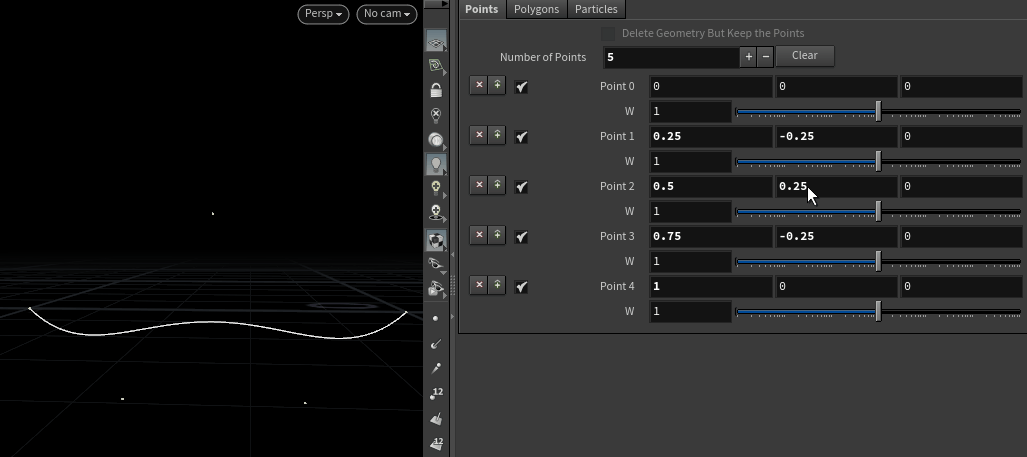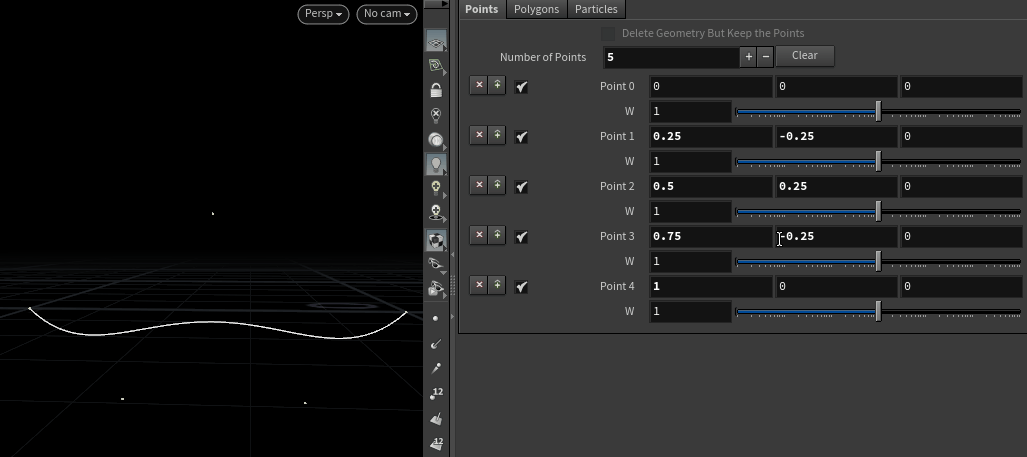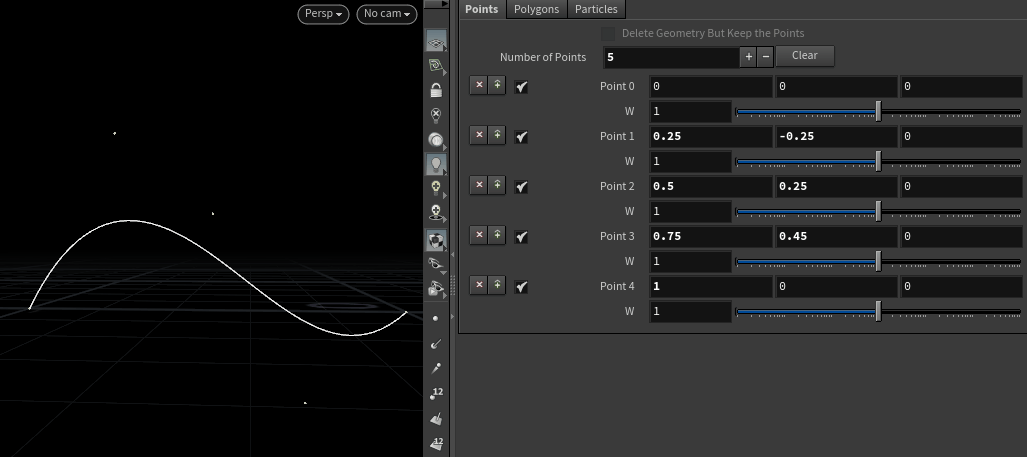
Bezier曲线在例如Photoshop中的钢笔工具等工业软件中有很重要的应用,可以帮助艺术家制作出一些直观上的光滑的曲线;其中最主要的部分是伯恩斯坦多项式,也就是下方代码中的
compute函数
这是个多项式喔。
Bernstein Polynomial.
vector compute(vector p1, p2; float t){
return (1-t)*p1+t*p2;
}
vector gen_bezier( vector p[]; float t ){
vector ps[] = p; // Note: p is reference, so we need a new variable
int iter = len(ps);
for(int z=0; z<iter; z++){
int n=len(ps);
vector tmp[];
for(int i=0;i<n-1;i++){
vector cr = vector(compute(ps[i], ps[i+1], t));
push( tmp, cr);
}
ps=tmp;
iter--;
}
return compute(ps[0], ps[1], t);
}
int step=chi("step");
float interval=1.0/step;
int prim0 = addprim(0, "polyline");
vector tp[];
int np = npoints(0);
int i=0;
while(i<np){
push(tp, vector(point(0, "P", i)));
i++;
}
for(float t=0;t<1;t+=interval){
int pt=addpoint(0, gen_bezier(tp, t));
addvertex(0, prim0, pt);
}
原理:
Bernstein多项式与概率密切相关(假设我们在做一个实验,做了n次,成功i次的概率是多少?怎么计算?就是上面的那个公式),我们知道假设的概率,概率的范围是[0,1],则我们多尝试一些,会有
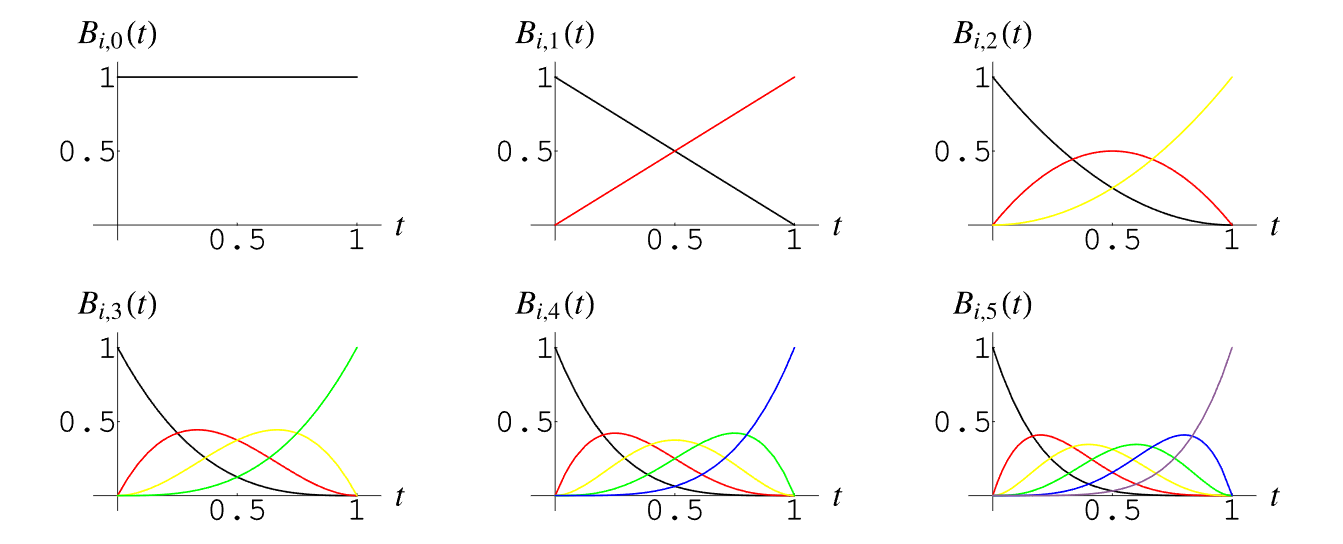
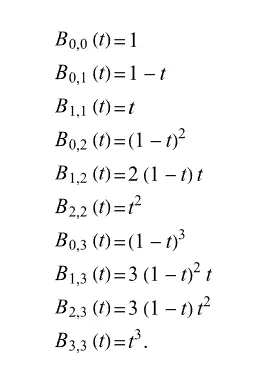
Bernstein Polynomial. Figure from - Wolfram MathWorld
它的值总是往所取值处的尖峰处靠拢,再进行迭代,就得到Bezier曲线了
贝塞尔曲线中的伯恩斯坦多项式(Bernstein Polynomial) - 知乎 - 前面的还能读懂,后面就只知其意,不知其理了。看来还是只能听懂大白话。
贝塞尔曲线入门 - 一个非常全的介绍贝塞尔曲线的网站。