Barycentric Coordinates

重心坐标

插值Interpolation

给一段距离，再选取这段距离上的一个区间并记刻度 $0 - 1$ ，然后使用插值我们可以计算出这段距离上的每一处的值，当在中间时，就是 $0.5$ ; 或者说我们将 $0$ 刻度处设为红色， $1$ 刻度处设为绿色，同样使用插值我们可以计算出这段距离上每一处的颜色，使用颜色混合，当在中间时，红色和绿色的强度是一样的，我们知道可以混合出黄色

重心坐标的引入

模型可以使用许多三角形来表示

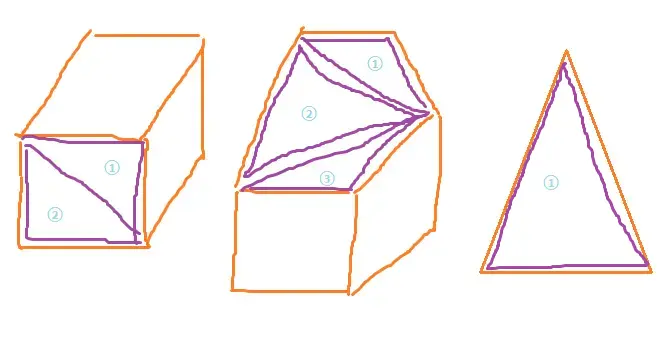
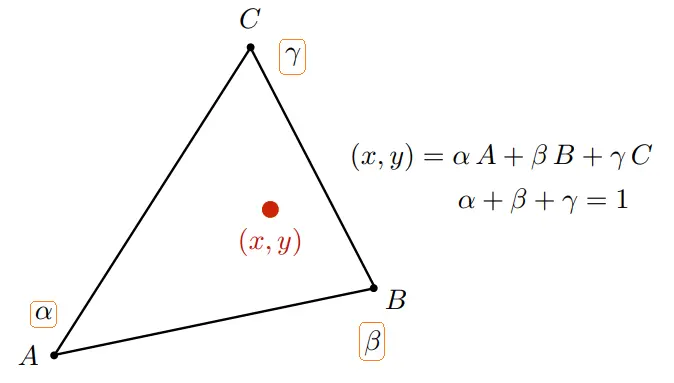
刚才举例中的在一段距离上插值两个颜色应用到三角形上该如何表示呢？答案是使用重心坐标,重心坐标就是在一个三角形内使用三个数值 ( $α β γ$ ),用这三个数值来表示这个三角形内每一个点的位置，并且需要满足这三个数值相加起来等于 $1$

用一种直观的感受，我们小时候应该玩过一种玩具，一个透明的塑料盖子里有一个迷宫，里面有一个小铁球，我们通过前后左右摆动来控制小铁球走出迷宫

将这个迷宫想象成三角形，当我们摇动时，这个小球就会前往这个三角形中不同的地方，是不是就是"重心"再往那个地方偏呢在，在数学中也是一样的道理。
现在我们向左下移动，那么这个小球就会"铛"的一声，停靠在左下方

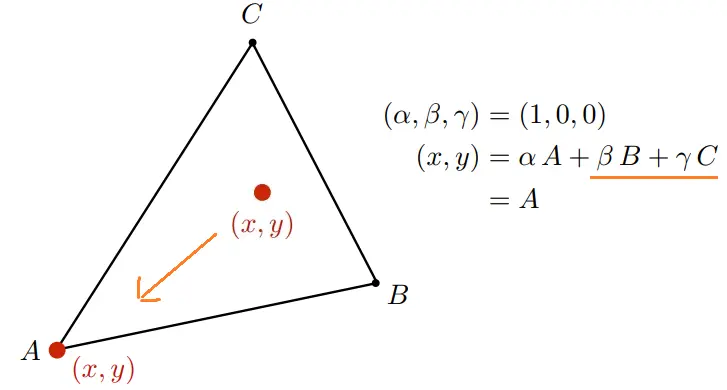
那么就像所有的"重心"都落在了左下方这个 $A$ 点上了，在数学上表示呢，就是 $α$ 的数值为 $1$ , $β$ 和 $γ$ 的值为 $0$

如何计算这个坐标

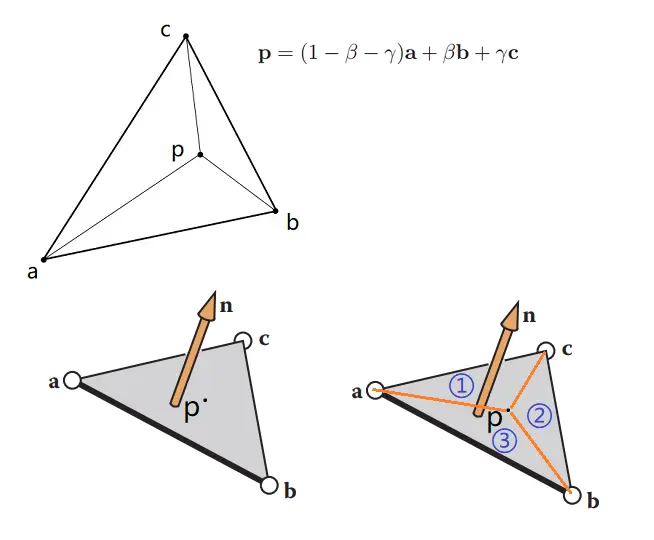
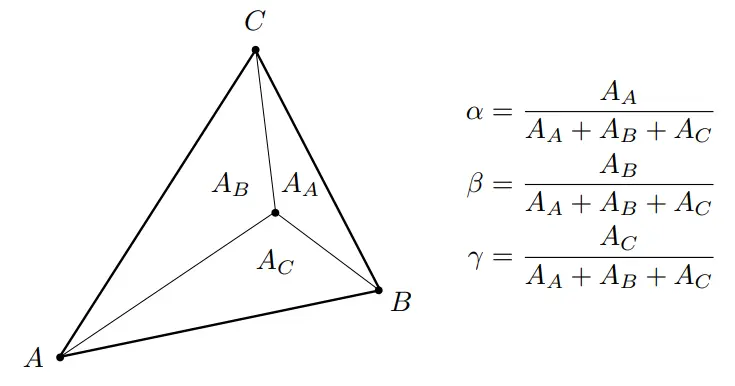
$P$ 点分别与三角形的三个顶点相连，我们可以得到三个小三角形，然后通过分别计算这个三个小三角形的面积与整个三角形的面积的比值

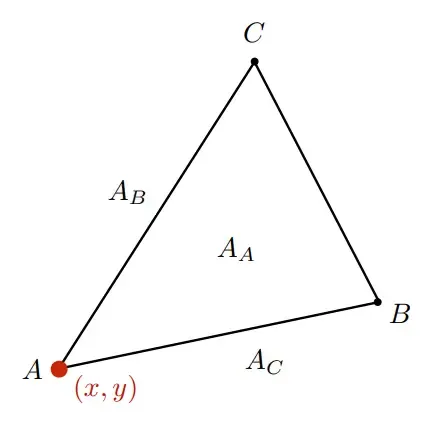
那么之前的那个例子通过计算就是小三角形 $A_{A}$ 占据了整个三角形，与整个三角形的面积比值为 $\frac{1}{1} = 1$ ,而小三角形 $A_{B}$ 与 $A_{C}$ 与整个三角形的面积比为 $\frac{0}{1} = 0$ ,现在的问题就是我们如何计算这个面积比值

首先是三角形上的法线计算，使用cross_product叉乘

n = (b - a) \times (c - a)

求得法线 (两个向量叉乘得第三个向量且垂直于这两个向量) 为什么要计算法线呢？因为计算法线与求面积有关,让我们继续往下看，在我们求得法线之后，我们就有三角形的面积为

a r e a = \frac{1}{2} | | n | |

这里为什么面积是 $\frac{1}{2}$ 倍的法线的模？抛开叉乘的几何意义，我们从代数意义去看叉乘

其中

‖ a \times b ‖ = ‖ a ‖ ‖ b ‖ \sin (θ)

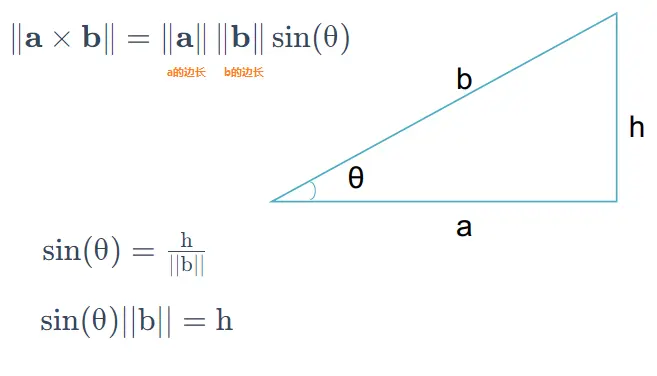
是叉乘的模长计算公式，其中 $a$ 向量的模也就是 $a$ 的边长， $b$ 向量的模就是 $b$ 的边长,根据三角形面积的计算公式

Δ = \frac{1}{2} a h

我们发现，计算叉乘的过程正好是计算三角形面积的过程，只不过少除以了一个 $2$ ，所以叉乘的模长的 $\frac{1}{2}$ 倍正好就是三角形的面积

计算其中两个小三角形的面积和整个三角形的面积，其中

①的面积为

\frac{1}{2} \times | | (a - p) \times (c - p) | |

②的面积为

\frac{1}{2} \times | | (b - p) \times (c - p) | |

整个三角形的面积为

\frac{1}{2} \times | | (b - a) \times (c - a) | |

则我们最终有

\begin{array}{l} α = \frac{① 的 面 积}{整 个 三 角 形 面 积} \\ β = \frac{② 的 面 积}{整 个 三 角 形 面 积} \\ γ = 1 - α - β \end{array}

注：计算方法不唯一，还有一些其它的计算方法

Connected Pages

Depth

Pages mentioning this page

Coordinate System