B Spline

Graphics-B Spline

B样条是贝塞尔曲线的推广，是由于Bezier曲线上的每一点会受到所有控制点的影响，我们称它为"全局的"，而B样条是一种"局部的"。

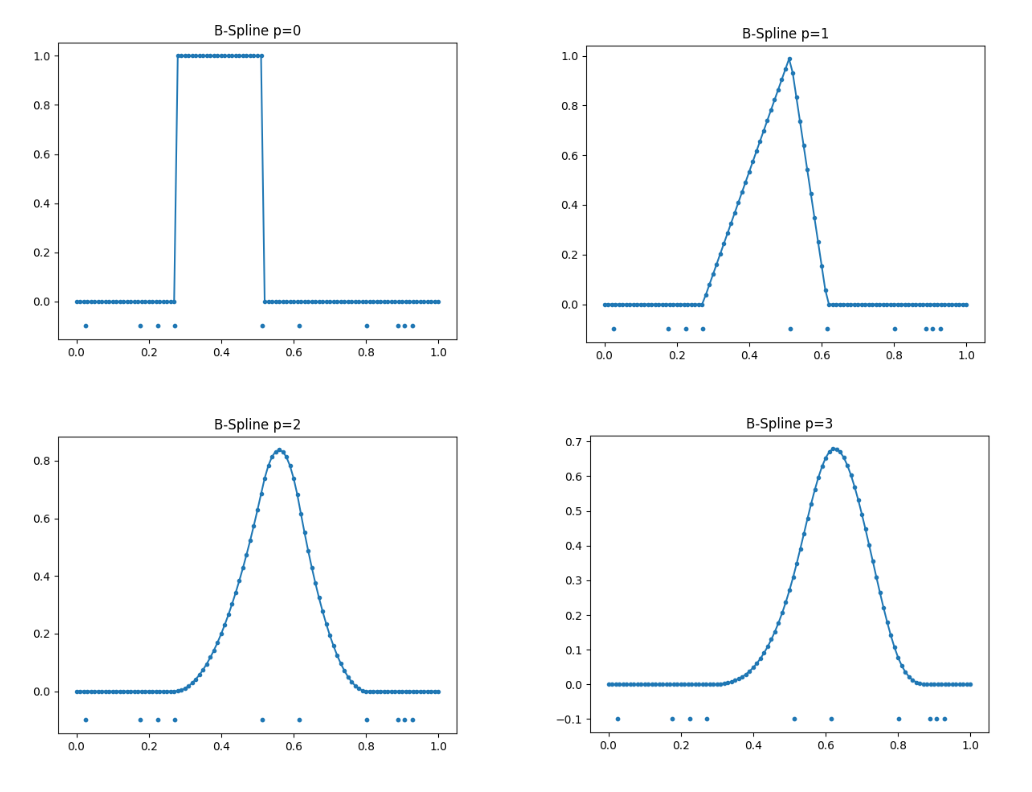
迭代公式与计算公式 (下方公式是离散情况下，其中k与代码中knotvector对应)

P (t) = \sum_{i = 0}^{n} P_{i} B_{i, p} (t), t \in [t_{k - 1}, t_{n - 1})

\begin{aligned} B_{(i, p, k)} (t) & = \frac{t - k_{i}}{k_{i + p} - k_{i}} B_{(i, p - 1, k)} (t) + \frac{k_{i + p + 1} - t}{k_{i + p + 1} - k_{i + 1}} B_{(i + 1, p - 1, k)} (t) \end{aligned}

\begin{aligned} B_{(i, 0, k)} (t) & = {\begin{cases} 1 (k_{i} \leq t < k_{i + 1}) \\ 0 (otherwise) \end{cases} \end{aligned}

Code


def SimpleBSpline(i, p, k, t):
     if p==0:
          return k[i] <= t <= k[i+1]  # return 0 or 1
     else:
          return SimpleBSpline(i, p-1, k, t) * (t-k[i])/(k[i+p]-k[i]) \
                 + SimpleBSpline(i+1, p-1, k, t) * (k[i+p+1]-t)/(k[i+p+1]-k[i+1])

def Simple_B_Spline():
     knotvector = []
     step = 100
     result = [0.0 for i in range(step+1)]
     points = 10
     t=0.0
     interval = 1.0/step
     randomRange = (0.0, 1.0)

     for i in range(points):
          knotvector.append(random.uniform(randomRange[0], randomRange[1]))
     knotvector.sort()
     knotvector = [0.026, 0.176, 0.226, 0.271, 0.513, 0.616, 0.802, 0.888, 0.905, 0.928]
     y = [-0.1 for i in range(points)]
     p=3  # order
     i=3
     x = [0.0 for i in range(step+1)]
     for j in range(step+1):
          t = j*interval
          x[j] = t
          result[j] += SimpleBSpline(i, p, knotvector, t)
     plt.title("B-Spline p=%s" % p)
     plt.plot(x, result, marker='.')
     plt.scatter(knotvector, y, s=10)
     plt.show()